TINY MACHINE LEARNING LEZIONE 8

CORSO TINY ML

INDICE

  1. Avvertenze
  2. Note sul Copyright
  3. Il Deep Learning e la Rete Neurale
  4. Funzioni di attivazione dei neuroni
  5. Funzione Sigmoidea
  6. Funzione Smoothstep
  7. Funzione Tangente Iperbolica – Tanh
  8. Funzione ReLU
  9. Definizione del Modello da addestrare per Hello World con Keras
  10. PAI-019: Modello di Hello World (Base)
  11. Addestramento del Modello Hello World (Base)
  12. Rappresentazione Grafica dei dati di addestramento
  13. PAI-020: Modello di Hello World (Migliorato)

Avvertenze

Relativamente agli aspetti di sicurezza, poiché i progetti sono basati su alimentazione elettrica in bassissima tensione erogata dalla porta usb del pc o da batterie di supporto o alimentatori con al massimo 9V in uscita, non ci sono particolari rischi di natura elettrica. È comunque doveroso precisare che eventuali cortocircuiti causati in fase di esercitazione potrebbero produrre danni al pc, agli arredi ed in casi estremi anche a ustioni, per tale ragione ogni qual volta si assembla un circuito, o si fanno modifiche su di esso, occorrerà farlo in assenza di alimentazione e al termine dell’esercitazione occorrerà provvedere alla disalimentazione del circuito rimuovendo sia il cavo usb di collegamento al pc che eventuali batterie dai preposti vani o connettori di alimentazione esterna. Inoltre, sempre per ragioni di sicurezza, è fortemente consigliato eseguire i progetti su tappeti isolanti e resistenti al calore acquistabili in un qualsiasi negozio di elettronica o anche sui siti web specializzati.

Al termine delle esercitazioni è opportuno lavarsi le mani, in quanto i componenti elettronici potrebbero avere residui di lavorazione che potrebbero arrecare danno se ingeriti o se a contatto con occhi, bocca, pelle, etc. Sebbene i singoli progetti siano stati testati e sicuri, chi decide di seguire quanto riportato nel presente documento, si assume la piena responsabilità di quanto potrebbe accadere nell’esecuzione delle esercitazioni previste nello stesso. Per i ragazzi più giovani e/o alle prime esperienze nel campo dell’Elettronica, si consiglia di eseguire le esercitazioni con l’aiuto ed in presenza di un adulto.

Roberto Francavilla

Il Deep Learning e la Rete Neurale

Prima di continuare nella realizzazione del nostro progetto di Machine Learning chiamato Hello World, ho bisogno di spiegarvi un po’ di teoria, ma, come dico sempre in questi casi, non vi preoccupate, sarò il più elementare possibile nella spiegazione (tanto, che i super esperti storceranno il naso…. ma non importa, so’ che capiranno).

Innanzi tutto vediamo il termine, “Deep Learning”, in Italiano si traduce con Apprendimento Profondo, ovvero un apprendimento che avviene in modo sequenziale su più livelli, partendo dal livello più esterno e via via andando sempre a livelli inferiori. Ogni livello è un “layer” (ovvero uno strato) composto da di “neuroni”. Già da questo è facilmente intuibile che più livelli ci sono e tanto più il mio modello imparerà meglio ad effettuare le sue previsioni con maggiore precisione, fino al punto che il modello non riuscirà ad imparare più nulla.

Il primo strato di neuroni è chiamato strato di Input, quelli sottostanti, si chiamano strati nascosti.

Facciamo una rappresentazione grafica di quanto detto sopra con un esempio di un modello relativo ad una stazione meteo che ha 6 dati di Input, poi ha un primo strato di 6 neuroni, un secondo strato di 4 neuroni e l’ultimo strato, con un neurone, con l’emissione dell’ Output, ovvero la previsione: se ci sarà sole o pioggia.

Questo modello è rappresentabile così:

Ogni neurone riceverà un input e tirerà fuori un output che va ad alimentare i neuroni dello strato sottostante.

Ingrandendo l’immagine relativa al neurone… vediamo cosa accade all’interno dello stesso neurone:

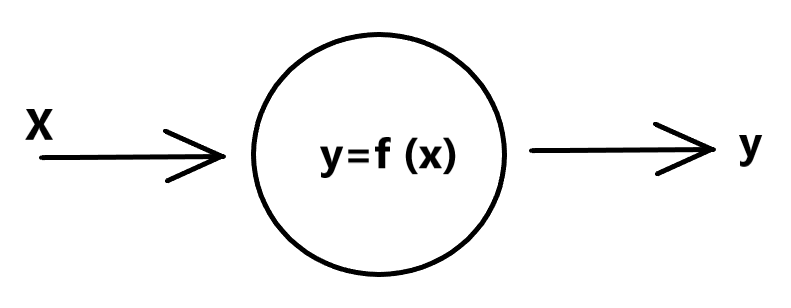
Vediamo che ad un valore x in ingresso al neurone, c’è un valore di y, in uscita, secondo una determinata funzione. Questa funzione si chiama funzione di attivazione del neurone e viene rappresentata come una funzione matematica generica y = f(x), cioè, ad un ingresso x, dal neurone ci sarà un output y. Quindi sostanzialmente una funzione di attivazione viene utilizzata per mappare l’ingresso all’uscita. Questa funzione di attivazione aiuta una rete neurale ad apprendere relazioni e schemi complessi nei dati.

Funzioni di attivazione dei neuroni

Nel Machine Learning ci sono tantissime funzioni di attivazione, i vari ricercatori e studiosi del mondo ML, trovano, ormai, quotidianamente nuove funzioni di attivazione in funzione dell’applicazione della stessa. Non è mia intenzione spiegavi come creare una “funzione di attivazione” perché è complesso e bisogna avere alla base studi matematici a livello universitario, ma vi spiegherò come utilizzare quelle già definite per i nostri progetti.

Giusto per cultura generale ed attingendo dall’immensa enciclopedia online Wikipedia (di cui sono sostenitore ed invito anche voi a fare donazioni) vi mostro alcuni esempi di funzioni di attivazione dei neuroni.

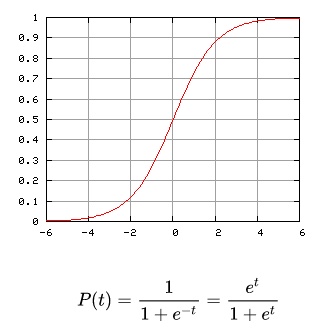
Funzione Sigmoidea

[Fonte: Wikipedia]

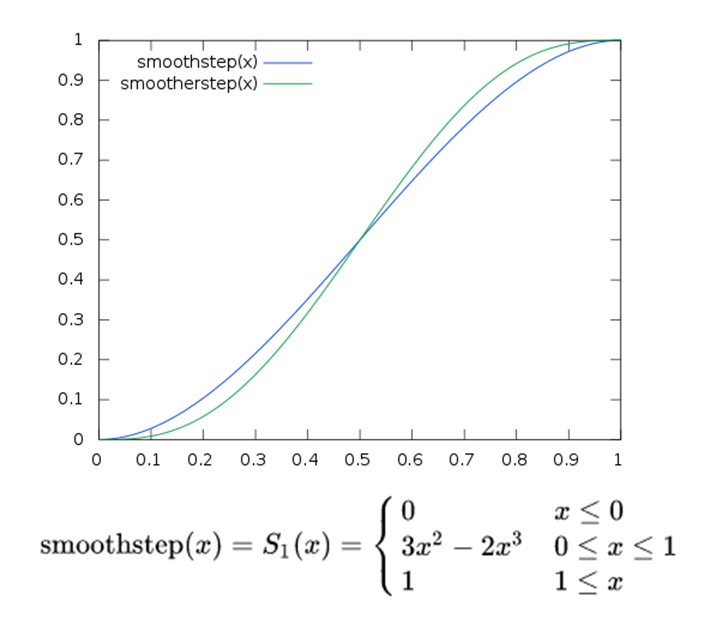
Funzione Smoothstep

[Fonte: Wikipedia]

Funzione Tangente Iperbolica – Tanh

[Fonte: Wikipedia]

Funzione ReLU

[Fonte: Wikipedia]

…. e tante altre…. ognuna di esse ha uno o più impieghi nel Machine Learning, ad esempio la funzione  Smoothstep è normalmente impiegata in quei modelli che si occupano di elaborazioni grafiche.

Noi, comunque, ci concentreremo su una, quella più semplice, tra quelle viste sopra, ovvero la funzione ReLU.

ReLU sta per Rectified Linear Unit, cioè Unità Lineare Rettificata. Quando una funzione di attivazione prende un valore di input (x) e restituisce un valore numerico di una funzione matematica (f(x), si dice che il modello ha una funzione di attivazione di regressione, o semplicemente ha una funzione di regressione o anche modello di regressione.

La ReLU è una particolare funzione di regressione, essa infatti assume un valore 0 per valori di x minore di 0 e per x =0 ed assume un valore pari ad x, per valori di x maggiore di 0.

Nel grafico in basso c’è la rappresentazione grafica con la tabella dei valori, si può osservare come per valori che vanno da -10 a 0 (incluso), la funzione restituisce valore 0, per valori di x maggiore di 0, la funzione restituisce un valore pari ad x.

Definizione del Modello da addestrare per Hello World con Keras

A questo punto abbiamo gli strumenti teorici per capire come creare il nostro modello da addestrare per il progetto Hello World.

Per cui i passi sono i seguenti:

  • Fissare il numero di strati di neuroni (in genere si va per tentativi, si inizia con due strati e poi si incrementa sin tanto il risultato migliora sensobilmente)
  • Inserire nel neurone la funzione di attivazione, che nel nostro caso sarà una funzione di regressione (utilizzeremo la ReLU)
  • Analizzeremo i risultati dell’apprendimento per verificare la necessità di azioni correttive e nel caso si passa alla compilazione per creare il codice TinyML.

Per la realizzazione del modello utilizzeremo un’altra risorsa del cloud, che in sostanza per noi sarà del tutto trasparente in quanto gestita attraverso il Notebook Colab. Questa risorsa si chiama Keras, ed è l’API (Application Programming Interface – Interfaccia di Programmazione delle Applicazioni) di alto livello di TensorFlow per la creazione di reti di deep learning.

 

Nota: Quanto riportato di seguito è frutto dell’elaborazione degli esempi messi a disposizione da TensorFlow ed in particolare al link:

https://www.tensorflow.org/lite/microcontrollers/get_started_low_level

e al link:

https://github.com/tensorflow/tensorflow/blob/be4f6874533d78f662d9777b66abe3cdde98f901/tensorflow/lite/experimental/micro/examples/hello_world/create_sine_model.ipynb

Rilasciata con licenza Apache 2.0

PAI-019: Modello di Hello World (Base)

Per cui, partiamo con il nostro progetto pratico.

Riprendiamo il nostro progetto Seno_Data.

Caricato il Notebook Seno_Data, copiamo le celle e le incolliamo in un nuovo Notebook, dopodiché nominiamo il nuovo Notebook come Seno_Function.

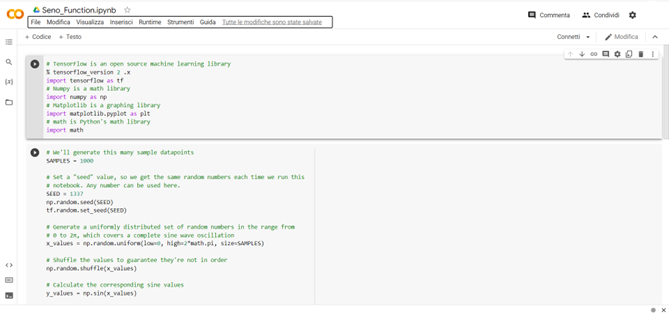
Aggiungiamo un’altra cella di codice e scriviamoci il seguente codice:

# We’ll use Keras to create a simple model architecture

from tensorflow.keras import layers

model_1 = tf.keras.Sequential()

# First layer takes a scalar input and feeds it through 16 “neurons”. The

# neurons decide whether to activate based on the ‘relu’ activation function.

model_1.add(layers.Dense(16, activation=’relu’, input_shape=(1,)))

# Final layer is a single neuron, since we want to output a single value

model_1.add(layers.Dense(1))

# Compile the model using a standard optimizer and loss function for regression

model_1.compile(optimizer=’rmsprop’, loss=’mse’, metrics=[‘mae’])

# Print a summary of the model’s architecture

model_1.summary()

Analizziamo riga per riga cosa stiamo facendo.

from tensorflow.keras import layers

Nella prima riga (sopra) stiamo attivando Keras per il rilascio degli strati di neuroni

model_1 = tf.keras.Sequential()

Nella seconda riga, stiamo dicendo a Keras che il modello che realizzeremo è di tipo sequenziale, ovvero che avremo almeno due strati di cui uno di input e l’atro profondo e che gli input saranno processati dal primo e passati sequenzialmente al secondo.

model_1.add(layers.Dense(16, activation=’relu’, input_shape=(1,)))

Con questa riga creiamo il primo strato e lo definiamo “Dense”, cioè denso, significa che tutti i 16 neuroni sono connessi (infatti uno strato di questo tipo è detto “completamente connesso”), la funzione di attivazione utilizzata è la ReLU e l’input è formato da un solo valore scalare. E’ opportuno precisare che con i comandi contenuti nella riga, appena descritta, il lavoro di tipo matematico è totalmente gestito e svolto da Keras e TensorFlow, per cui da parte nostra non dobbiamo assolutamente introdurre null’altro di quanto già scritto nel codice.

model_1.add(layers.Dense(1))

Con la riga di codice sopra, aggiungiamo un ulteriore strato composto da un solo neurone completamente connesso con i neuroni dello strato precedente. Quindi il neurone riceverà 16 input, uno per ciascuno dei neuroni nello strato precedente.

Come potete osservare, per questo strato non è stata indicata nessuna funzione di attivazione, quindi il neurone non si attiverà e si limiterà a fare una media ponderata dei valori ricevuti (ovviamente questo sempre in modo trasparente al nostro codice). Quindi al termine dell’elaborazione ci sarà l’output.

Il ciclo completo dall’input (valore iniziale) all’output (valore finale) è chiamato, come abbiamo detto nelle lezioni precedenti, “inferenza” e ad ogni ciclo di inferenza (per il progetto Hello World, abbiamo previsto 1000 dati di input, per cui 1000 cicli d inferenza) TensorFlow, grazie alla funzione di attivazione, provvederà automaticamente a modificare i pesi da attribuire ai singoli valori durante l’attività dei neuroni.

model_1.compile(optimizer=’rmsprop’, loss=’mse’, metrics=[‘mae’])

La riga di codice sopra riguarda la compilazione, in sostanza con la funzione “optimizer” specifichiamo il tipo di algoritmo (‘rmsprop’) utilizzato, mentre gli argomenti ‘mse’ e ‘mae’ sono due funzioni di tipo statistico che indicano rispettivamente per la funzione “loss” il criterio di misura dell’errore quadratico medio, mentre per la “metrics”, il criterio dell’errore assoluto medio. Queste funzioni normalmente sono scelte per tentativi, comunque per i modelli di regressione, tipo il nostro, normalmente sono utilizzati i parametri definiti nella riga di codice scritta. Per maggiori approfondimenti su questi aspetti si può fare riferimento alla bibliografia che accompagna Keras.

model_1.summary()

Con l’ultima riga diciamo di stampare un sommario delle caratteristiche del modello.

A questo punto facciamo girare le singole celle cliccando sul simbolino del play posto su di ognuna di esse.

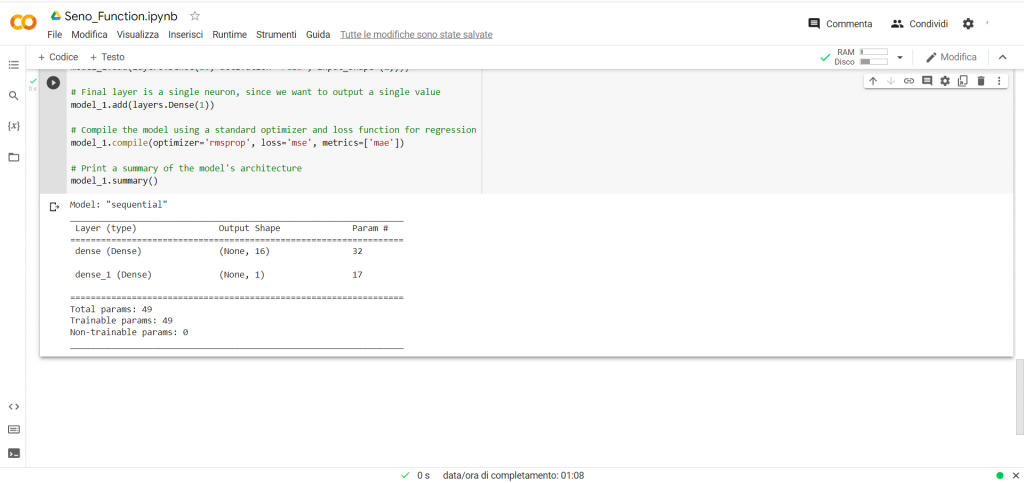
Nella foto sopra solo i risultati finali dell’ultima cella.

Addestramento del Modello Hello World (Base)

A questo punto passiamo all’addestramento, anche in questo caso sfrutteremo la potenza di Keras per semplificare il processo, infatti basta richiamare una semplice funzione “fit ( …. )”, passando tutti i parametri necessari, che si ha l’addestramento del modello.

Vediamo come fare…

Aggiungiamo sul Notebook un’altra cella di codice e scriviamoci il seguente codice:

# Train the model on our training data while validating on our validation set

history_1 = model_1.fit(x_train, y_train, epochs=1000, batch_size=16,

                    validation_data=(x_validate, y_validate))

 

Vediamo in dettaglio che cosa abbiamo scritto:

assegniamo l’output della funzione fit applicata al nostro model_1, ad una variabile denominata (arbitrariamente) history_1. In questa variabile (che sarà una matrice di valori) avremo tutta la storia dell’addestramento, per cui sarà importante analizzarla.

Come parametri alla funzione fit () inseriamo i due array per il training: x_train e y_train (vi ricordo che i due array hanno 600 elementi ognuno).

Poi stabiliamo l’epochs, cioè il numero di volte che il modello farà girare i dati di training. In questo caso è 1.000 (quindi ci saranno 600 x 1.000 , cioè 600.0000 inferenze). Il numero di epochs deriva dall’esperienza e dalla sperimentazione, infatti non bisogna mettere un numero troppo basso, altrimenti il modello non “impara” bene e non bisogna mettere un numero troppo elevato, altrimenti si ha l’ “overfitting” (cioè, quando il modello è capace di effettuare una previsione perfetta sulla base dei dati di training, ma non è capace di fare previsione su nuovi dati di input). Per cui è suggeribile partire con un valore di 1.000 e poi eventualmente perfezionare questo numero fin quando non si avrà alcun miglioramento nell’apprendimento da parte del modello.

Il parametro successivo è il batch_size, cioè stabiliamo il numero di lotti di dati di training che vengono immessi nel modello e quindi a valle di tale inferenza, far verificare gli scostamenti della previsione rispetto ai dati di test.

Anche in questo caso l’esperienza suggerisce di utilizzare il numero di neuroni del primo strato come batch_size, in questo modo avremo, per i 600 dati di traininig, 38 momenti di verifica (cioè 600 : 16) con cambio automatico dei pesi e della distorsione nel modello e considerando che abbiamo scelto come epochs il valore di 1.000, avremo 38.000 momenti di potenziale miglioramento del modello. Mi preme precisare che l’aver fissato come valore di batch_size=16 vale in questo caso, ma potrebbe non essere un valore corretto per altri modelli, per cui anche per questo valore occorre fare diversi tentativi e sperimentare i risultati prima di fissarlo definitivamente. Per alcuni modelli, soprattutto quando si usano un numero maggiore di 16 di neuroni nel primo strato, al batch_size viene assegnato un valore 32.    

Infine l’ultimo parametro della funzione fit è il set di dati di validazione con validation_data.

Questo set di dati vengono forniti e fatti elaborare dal modello, per due motivi:

  • per non incorrere nell’overfitting, infatti dopo i dati di training, si danno in pasto al modello delle previsioni da fare sulla base di nuovi input
  • per misurare gli scostamenti dei valori di previsione, effettuata dal modello in fase di addestramento, e il risultato reale già validato.

Come è possibile osservare, per questo addestramento, non vengono utilizzati, in questa fase, i dati di test che avevamo predisposto nella Lezione 7, infatti non sempre è necessario utilizzare i dati di test per l’addestramento (che sono un ulteriore set di dati “nuovi” per evitare l’overfitting e per migliorare l’addestramento).

A questo punto lanciamo il codice contenuto nella cella cliccando sul play in alto a sinistra e comparirà l’elaborazione che richiederà qualche minuto:

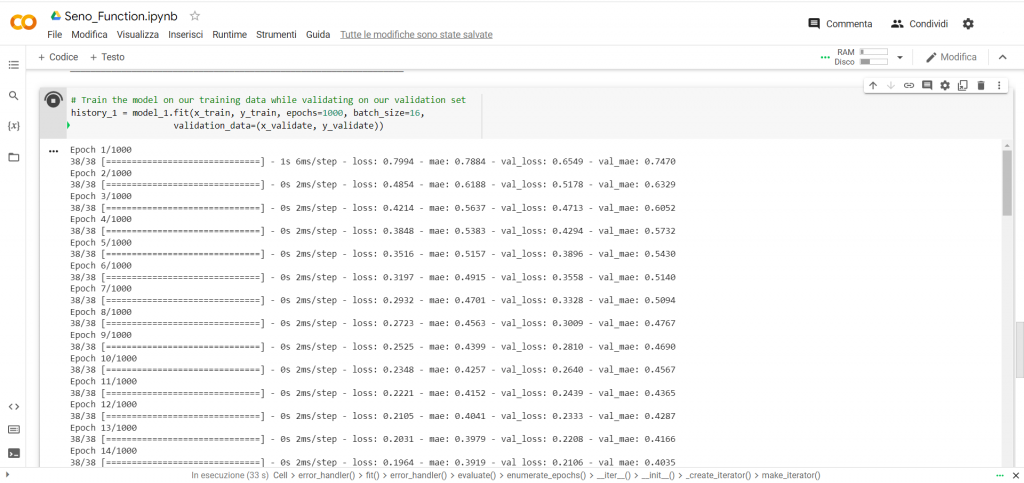
Al termine dell’elaborazione il nostro modello è stato addestrato.

Andiamo ad analizzare i valori generati durante l’addestramento e focalizziamo la nostra attenzione sull’evolversi dei seguenti valori:

  • Loss; cioè l’errore quadratico medio (è una particolare media con valori sempre positivi) che commette il modello nell’effettuare la sua previsione sulla base dei valori di training
  • Mae; cioè il valore dell’errore assoluto (anch’esso sempre positivo) che commette il modello nell’effettuare la sua previsione sulla base dei valori di training
  • Val_loss; cioè l’errore quadratico medio che commette il modello nell’effettuare la sua previsione sulla base dei valori di validazione
  • Val_mae; cioè il valore dell’errore assoluto che commette il modello nell’effettuare la sua previsione sulla base dei valori di validazione

Come è possibile osservare, il valore “loss” va sostanzialmente a decrescere, come anche il “mae”, questo significa che il modello sta imparando a fare previsioni sempre più precise. Osserviamo e confrontiamo adesso i valori di “mae” e “val_mae” e si può osservare come i valori sono molto simili, ma quelli di “mae” sono più piccoli di quelli di “val_mae”. Questo significa che il modello sta imparando a fare previsioni migliori con i dati di training rispetto a quelli di validazione. Per cui il modello sta andando nella direzione di overfitting.

Comunque, nonostante il nostro modello abbia imparato qualcosa e stia andando in overfitting, l’errore è ancora molto alto. Infatti commettere un errore, in termini assoluti, di 0,3 su un valore di seno che può avere un valore che oscilla tra -1 e +1, significa commettere un errore del 30% e questo è per noi non accettabile. Per cui proviamo a migliorare il nostro modello.

Prima di passare al miglioramento del modello, vediamo come rappresentare graficamente i dati che vengono immagazzinati durante la fase di addestramento.

Rappresentazione Grafica dei dati di addestramento

Aggiungiamo una cella di codice e ricopiamo il seguente codice:

# Draw a graph of the loss, which is the distance between

# the predicted and actual values during training and validation.

loss = history_1.history[‘loss’]

val_loss = history_1.history[‘val_loss’]

epochs = range(1, len(loss) + 1)

plt.plot(epochs, loss, ‘g.’, label=’Training loss’)

plt.plot(epochs, val_loss, ‘b’, label=’Validation loss’)

plt.title(‘Training and validation loss’)

plt.xlabel(‘Epochs’)

plt.ylabel(‘Loss’)

plt.legend()

plt.show()

Andiamo a capire cosa abbiamo scritto; la variabile history_1 che avevamo definito nella cella precedente con la funzione di addestramento, man mano che viene riempita conserva anche i valori di errore, per cui con le righe:

loss = history_1.history[‘loss’]

val_loss = history_1.history[‘val_loss’]

andiamo ad estrarre i valori degli errori.

Con la riga:

epochs = range(1, len(loss) + 1)

andiamo a definire il range di visibilità, cioè 1000+1.

Dopodiché con i comandi plot, title, xlabel, ylabel e legend facciamo stampare il grafico che mostrerà gli errori man mano che il modello viene addestrato.

A questo punto lanciamo il codice contenuto nella cella e si ottiene:

Come è possibile vedere dal grafico, già dopo i primi 100 valori di epochs si ha una stabilizzazione dell’errore ed il modello non impara più nulla (si ha l’overfitting), per cui per capire meglio il punto dove il modello non impara più nulla, andiamo a rappresentare graficamente i valori degli errori dopo le prime 100 epochs.

Aggiungiamo un’altra cella di codice e scriviamo:

# Exclude the first few epochs so the graph is easier to read

SKIP = 100

plt.plot(epochs[SKIP:], loss[SKIP:], ‘g.’, label=’Training loss’)

plt.plot(epochs[SKIP:], val_loss[SKIP:], ‘b.’, label=’Validation loss’)

plt.title(‘Training and validation loss’)

plt.xlabel(‘Epochs’)

plt.ylabel(‘Loss’)

plt.legend()

plt.show()

Con la funzione “skip” non facciamo altro che saltare le prime 100 posizioni e quindi viene rappresentato graficamente tutto ciò che accade dalla 101 in poi:

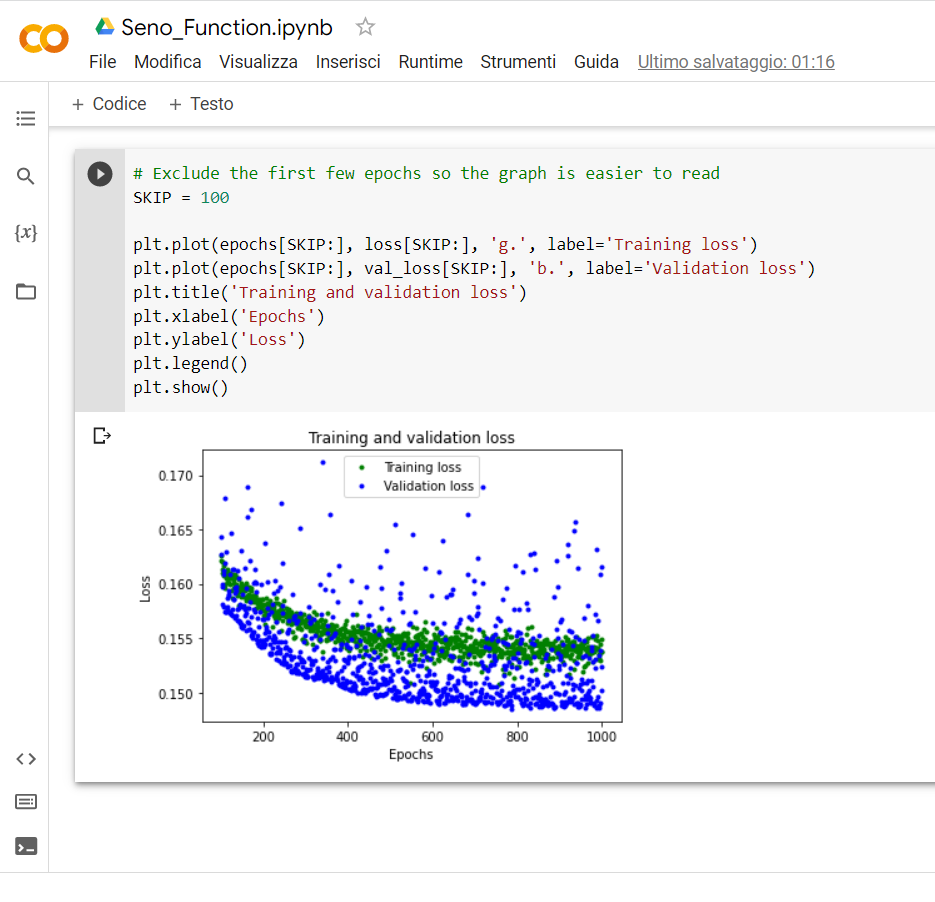
Con questa rappresentazione noi stiamo confrontando i valori medi dell’errore, nel caso si desiderasse visualizzare i valori dell’errore in termini assoluti, allora occorre aggiungere ancora qualche riga di codice, per cui aggiungi una ulteriore cella e scriviamoci il seguente codice:

# Draw a graph of mean absolute error, which is another way of

# measuring the amount of error in the prediction.

mae = history_1.history[‘mae’]

val_mae = history_1.history[‘val_mae’]

plt.plot(epochs[SKIP:], mae[SKIP:], ‘g.’, label=’Training MAE’)

plt.plot(epochs[SKIP:], val_mae[SKIP:], ‘b.’, label=’Validation MAE’)

plt.title(‘Training and validation mean absolute error’)

plt.xlabel(‘Epochs’)

plt.ylabel(‘MAE’)

plt.legend()

plt.show()

In sostanza, quanto scritto sopra, è lo stesso codice della cella precedente solo che al posto dei valori di loss e val_loss, vengono rappresentati graficamente i valori di “mae” e “val_mae”. Lanciando il play si ottiene:

Questo grafico rappresenta il valore assoluto (sempre positivo) dell’errore dato dalla differenza tra valore atteso per i dati di training e i valori previsti e il valore assoluto dell’errore tra il valore di validazione e quelli previsti. Come è possibile osservare la curva blu, dopo l’epochs 600, assume una direzione leggermente diversa dalla curva con i punti verdi e tende a stare sopra. Questo significa che il modello smette sostanzialmente di imparare, in quanto l’errore resta mediamente identico, e che nei dati di previsione dai dati di training c’è un errore leggermente minore rispetto alle previsioni effettuate con i dati di validazione, cioè si sta evidenziando l’overfitting. Inoltre, poiché l’errore ha un valore di circa 0,3 su un valore reale di 1 (valore massimo assoluto dell’onda sinusoidale), questo significa che il modello sta commettendo un errore del 30% circa.

Nell’analisi dei dati che stiamo facendo, è opportuno anche effettuare un confronto diretto fra valore di previsione, sulla base dei dati di input del training e valore effettivo. Per questa analisi usiamo i dati di test. Quindi aggiungiamo un’altra cella di codice e scriviamo il codice sotto:

# Use the model to make predictions from our validation data

predictions = model_1.predict(x_train)

# Plot the predictions along with to the test data

plt.clf()

plt.title(‘Training data predicted vs actual values’)

plt.plot(x_test, y_test, ‘b.’, label=’Actual’)

plt.plot(x_train, predictions, ‘r.’, label=’Predicted’)

plt.legend()

plt.show()

La riga importante su cui desidero soffermarmi è la seguente:

predictions = model_1.predict(x_train)

in questa riga noi estraiamo i dati di previsione che ha effettuato il nostro modello, questi dati vengono acquisiti in una variabile chiamata “predictions” e l’estrazione è effettuata con la funzione “predict” applicata al nostro modello che si chiama “model_1” sulla base dei dati di input dell’”x_train”.

I valori di confronto, invece, sono semplicemente la coppia “x_test” e “y_test”.

Cliccando su play, si ottiene:

Questo grafico ci dà un’informazione importantissima, come si può osservare dalla curva rossa (che è praticamente una retta), il modello non riesce ad effettuare una previsione corretta (curva in blu), questo significa che il modello non è in grado di imparare oltre un certo limite, cioè non ha sufficienti neuroni.

In conclusione dall’analisi dei grafici sopra emergono due cose importanti:

  • Il modello non riesce ad apprendere oltre un certo livello
  • Dopo le 600 epochs si va in overfitting

PAI-020: Modello di Hello World (Migliorato)

Sulla base delle considerazioni precedenti andiamo ad effettuare quei miglioramenti richiesti per far si che la previsione del modello sia più vicina possibile ad una sinusoide.

Per prima cosa riprendiamo il Notebook Seno_Function e salviamo un copia su Drive, per fare questo: File -> Salva una Copia su Drive

Verrà aperto un nuovo Notebook di nome “Copia_Seno_Function” e quindi provvediamo a rinominarlo con “Seno_Functon_2”.

A questo punto, la prima azione da fare per migliorare il modello è quella di implementare un nuovo strato di neuroni, anzi poiché la previsione si discosta di molto dai dati attesi, aggiungiamo due nuovi strati di neuroni (è come se gli stessimo dando al modello più materia celebrale, cioè un cervello più grande!). Per fare questo andiamo nella cella dove abbiamo definito il modello e modifichiamo la cella sostituendo il codice presente con questo che segue:

# We’ll use Keras to create a simple model architecture

from tensorflow.keras import layers

model_2 = tf.keras.Sequential()

# First layer takes a scalar input and feeds it through 16 “neurons”. The

# neurons decide whether to activate based on the ‘relu’ activation function.

model_2.add(layers.Dense(16, activation=’relu’, input_shape=(1,)))

# The new second layer 

model_2.add(layers.Dense(16, activation=’relu’))

# The new third layer 

model_2.add(layers.Dense(16, activation=’relu’))

# Final layer is a single neuron, since we want to output a single value

model_2.add(layers.Dense(1))

# Compile the model using a standard optimizer and loss function for regression

model_2.compile(optimizer=’rmsprop’, loss=’mse’, metrics=[‘mae’])

# Show a summary of the model

model_2.summary()

Come potete osservare, rispetto al precedente modello chiamato model_1, questo nuovo modello chiamato model_2, ha due strati da 16 neuroni aggiuntivi e vengono definiti come i precedenti, ovvero con la riga:

# The new second layer 

model_2.add(layers.Dense(16, activation=’relu’))

# The new third layer 

model_2.add(layers.Dense(16, activation=’relu’))

Come è possibile osservare, in questa definizione degli ulteriori strati, non occorre precisare l’input, in quanto essendo strati sequenziali, le uscite dai 16 neuroni sono combinate automaticamente dal modello come ingresso per il successivo strato sempre da 16 neuroni.

A questo punto andiamo a modificare il codice nelle altre celle seguenti considerando che al posto della variabile model_1, occorrerà inserire model_2, al posto di history_1, occorrerà inserire history_2 e per quanto riguarda le epochs, porre tale valore da 1000 a 600.

Per quanto sopra il codice nelle varie celle sottostanti diventa:

# Train the model on our training data while validating on our validation set

history_2 = model_2.fit(x_train, y_train, epochs=600, batch_size=16,

                    validation_data=(x_validate, y_validate))

__________________________________________________________

# Draw a graph of the loss, which is the distance between

# the predicted and actual values during training and validation.

loss = history_2.history[‘loss’]

val_loss = history_2.history[‘val_loss’]

epochs = range(1, len(loss) + 1)

plt.plot(epochs, loss, ‘g.’, label=’Training loss’)

plt.plot(epochs, val_loss, ‘b’, label=’Validation loss’)

plt.title(‘Training and validation loss’)

plt.xlabel(‘Epochs’)

plt.ylabel(‘Loss’)

plt.legend()

plt.show()

__________________________________________________________

# Exclude the first few epochs so the graph is easier to read

SKIP = 100

plt.plot(epochs[SKIP:], loss[SKIP:], ‘g.’, label=’Training loss’)

plt.plot(epochs[SKIP:], val_loss[SKIP:], ‘b.’, label=’Validation loss’)

plt.title(‘Training and validation loss’)

plt.xlabel(‘Epochs’)

plt.ylabel(‘Loss’)

plt.legend()

plt.show()

__________________________________________________________

# Draw a graph of mean absolute error, which is another way of

# measuring the amount of error in the prediction.

mae = history_2.history[‘mae’]

val_mae = history_2.history[‘val_mae’]

plt.plot(epochs[SKIP:], mae[SKIP:], ‘g.’, label=’Training MAE’)

plt.plot(epochs[SKIP:], val_mae[SKIP:], ‘b.’, label=’Validation MAE’)

plt.title(‘Training and validation mean absolute error’)

plt.xlabel(‘Epochs’)

plt.ylabel(‘MAE’)

plt.legend()

plt.show()

__________________________________________________________

# Use the model to make predictions from our validation data

predictions = model_2.predict(x_train)

# Plot the predictions along with to the test data

plt.clf()

plt.title(‘Training data predicted vs actual values’)

plt.plot(x_test, y_test, ‘b.’, label=’Actual’)

plt.plot(x_train, predictions, ‘r.’, label=’Predicted’)

plt.legend()

plt.show()

__________________________________________________________

Effettuate le modifiche clicchiamo su: Modifica à Cancella tutti i dati

E poi su: Runtime -> Riavvia ed esegui tutte [verrà chiesto di confermare, cliccate su SI]

Il risultato è stupefacente:

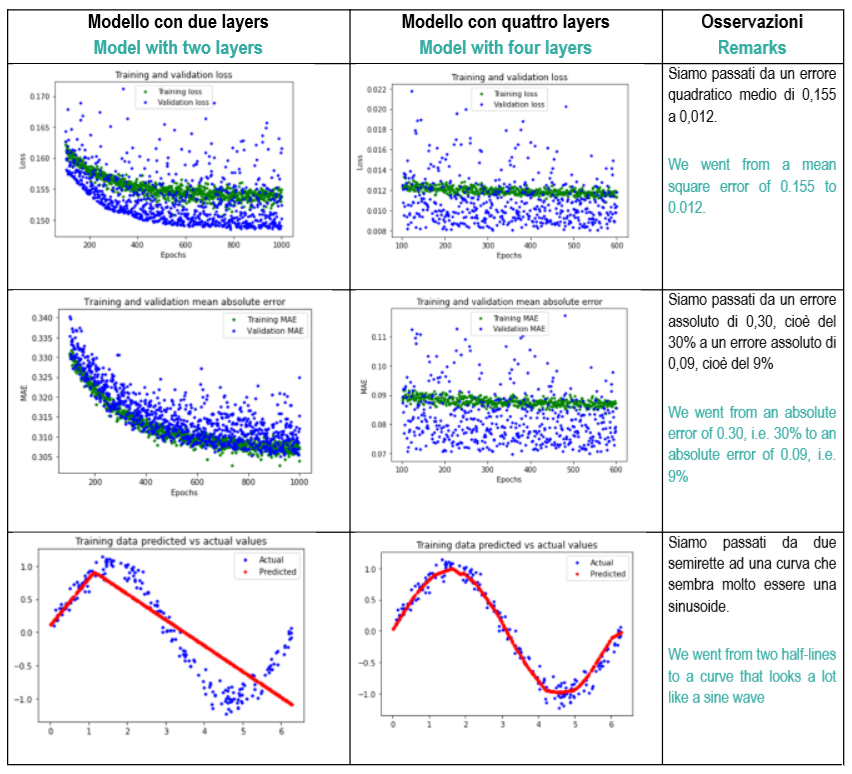
Inoltre desidero far osservare come la distribuzione dei valori di previsione derivante dai dati di training (curva in verde) siano leggermente superiori a quelli di validazione (curva in blu), questo significa che è sostanzialmente scomparso l’overfitting.

L’ultimissima cosa, per concludere la lezione che desidero farvi osservare, è che per realizzare un modello di autoapprendimento funzionante, come avete visto, sostanzialmente si procede per tentativi , sulla base della sperimentazione… per cui vi lascio con i vostri approfondimenti ed eventuali ulteriori miglioramenti.

Se hai trovato la lezione interessante fai una donazione mi aiuterai a realizzarne tante altre.

DONAZIONI